Hey folks, Sarge here [refering to my alias online - S0m3_random_guy, abbriviated to SRG which i like to pronounce as “Sarge” - just so you know.]
I’ve figured today is the day to put out something productive so I created a small testing game where I created a prototype system for aiming.
The prototype
Here you can take a look at the finished project. If you wish, you can remix it, reuse it, modify it or even just glance at the code to learn something new. Just make sure you credit my handle (@S0m3_random_guy) or Sarge as the creator of the aiming system (that is assuming you use this one as the basis for your game).
Disclaimer: I highly recommend going through this post before accessing this prototype to understand how it works
How to use
Movement
To move your player around use the arrow (←↑↓→) keys, for their respective directions.
Aiming & Shooting
Use the P2 left and right (jl) keys for moving the aim indicator leftwards and rightwards on the circular path. Press the A button (space or q) to fire green points from the player. (this is a placeholder projectile, feel free to replace it with any sprite of your choosing)
Explanation
This project involved some work other than coming up with the code, so I’ll show you how I assembled this prototype. Through this showcase/tutorial, we’ll go over these steps together:
- Figure out what the problem is
- Find a way to fix the problem
- Understand how to build our solution
- Code the solution in MakeCode Arcade
Brainstorming and Projecting
Before I create the code for the project, I must first establish an idea, and create an approach to solving the problem at hand. Then we can find the necessary formulas and implement them into our idea to make it work. At last, we can take the knowledge we have and the idea we’ve made to the next chapter.
Let’s get at it then, shall we?
The problem
MakeCode shooters often make it hard to aim where (or at what) your projectile is heading at. That’s because the player always fires in the same direction. This makes it significantly harder to hit your enemies from a distance without getting hurt yourself.
So what's the solution?
There are many ways to create an aiming system in a 2D landscape. The way you approach it yourself is up to you, but I’ll follow my way for this showcase (obviously lol). You can try to think of some yourself, and then I can reveal some ideas I’ve thought of myself:
- Free aim, anywhere on the screen
- n-way aiming system (any number can be substituted for n, which means we could have a 4-way aiming system such as up, down, left, right etc.)
- 360° circular path aiming system
- grid based system
Some of these systems have flaws and restraints, which I’ll explain now.
Free aim seems like a good choice initially, but soon you’ll realize it’s far too overpowered as it allows the player to shoot to usually unreachable places. It’s also common for the crosshair to drift away from the player which can be annoying. It’s also hard to determine where the projectiles should go when coding.
n-way (ex. 4-way) aiming system is a system constrained by the fact it’s hard coded to a few select directions, making it little, or even no better than a straight beam.
grid based system: (who the hell even uses those?)
You might have guessed already, but i’m going for the 360° circular path system simply because of how flexible it is. As we’ll see shortly, being the best way also makes it the hardest to create.
How to approach the problem
Now that we’ve decided on a system, it’s time to understand how it works. Since we’re aiming using a crosshair that spins around the player, we need to find a way to convert degrees into (x, y) coordinates.
Now is a good time to mention that this tutorial will contain some math and simple trigonometry, but it should be pretty straight-forward. I’ll also do my best to explain everything as well as I possibly can.
In order to create a 360° system we will need to first create an imaginary circle around the player. The circle we create will have radius r, which you can set to any value. The bigger r is, the farther the indicator will hang from the player.
Now we can take any amount of degrees and use it to calculate (x, y) on the coordinate system using some formulas. I got my formulas from the video below, made by Mathispower4u on YouTube. (vid. 1) in which their meaning is explained fairly well. I recommend watching it if you are unfamiliar with trigonometry or you want to expand your knowledge.
![]() Video 1 - finding (x, y) coordinates on a circle
Video 1 - finding (x, y) coordinates on a circle
From the linked video, we learn that the two main formulas we need are:
x = r x cos(degrees)
y = r x sin(degrees)
We will be making use of these formulas later. For now we need to find out how are we going to calculate using degrees.
Degrees & radians
In math, there are two ways of doing notation for circle circumference. Most people are familiar with the degree system - 360° make up a whole circle circumference. (I even used them in the title!) This, however isn’t possible to calculate using calculators or computers naturally. The degrees first have to be converted to radians (which are more “standard” ways of calculating circle circumference).
In the radian system, 360° = 2π (pi). This means one degree would be equivalent to π / 180 (or 2π / 360, the first way is just shortened). From this point multiplying the result (roughly ~0.017) with the number of degrees we want and you’ve successfully converted from degrees to radians! You can play around with the degree to radian calculator (linked below, res. 1)
Degrees to radians - calculator/converter
![]() Resource 1 - RapidTables.com degree to radian calculator
Resource 1 - RapidTables.com degree to radian calculator
Applying the formulas
In order to turn our idea into a reality, we will need to put what we’ve learned so far together. What you might notice if you try to implement this now, is that the circle is positioned on a path around 0, 0. This is because the formulas we calculated work on a circle positioned on (0, 0) in the coordinate system. This means we’ll have to add our player’s x and y position to the results of the formulas in order to center the aiming indicator (or crosshair) at the player.
Finally, we’ll need a way to control this aiming system. For ease of use, since our player’s movement is bound to the P1 joystick, I set the crosshair controls to the P2 L & R buttons. (j and l keys on your keyboard). We’ll work on implementing this in the next chapter of this tutorial (down below, it’s where i explain the programming and implementation) because it’s mostly changing variables and values. Before we proceed to the next chapter, try implementing this yourself, just to test if you understood and grasped what I’ve shown you here. If you don’t succeed immediately, don’t fret too much, as we’ll go over it together anyway, and you can always cross reference this post for more details.
Implementation in MakeCode Arcade (blocks)
Now that we’ve established what kind of system we want to create and how we’re going to approach it, we have to code it up in MakeCode. For this tutorial, I’ll be using Blocks, but i might create an update in the future where I’ll implement this in JavaScript (TypeScript) / Python.
Initiating sprites & variables
To start, we’ll define some variables and create the necessary sprites. We know we’ll need to keep track of the radius of our circle and the amount of degrees. For convenience we’ll also add the aim_sensitivity variable. (img. 1)
After that, we can add our character player sprite, and initialize it’s z-index, screen bounds and make it controllable. (img. 2)
Now we just create the aim (crosshair) sprite and change the background color to our liking. (img. 3)
Converting degrees to radians
Now we have to create a method (function) for converting degrees into radians. We’ll need a number input as an argument (deg), and a numeric return value. We’ll name the function degree_to_radian. (img. 1)
I already outlined the basics of degrees and radians in the previous chapter, so we now have to simply apply our formula and program it into this function. We have to return (π / 180) * deg, or pi divided by 180, and multiplied by deg, our argument. We can then return that value. (img. 2)
I used the Sprite utils extention by @jwunderl to get the value of π in my function, but you can also just default it to 3.14 (not tested, could be unstable or incorrect).
Making the controls
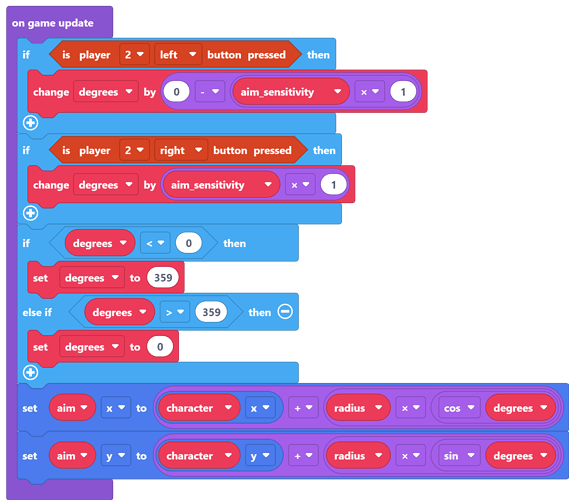
Since we want the contols to be held down, we can’t use the on <button> pressed block. Instead, we will be checking if each button is pressed every frame using the on game update method. When we press the P2 left button (j), we will decrease the degrees variable. We will do the opposite on the press of the P2 right button (l). (img. 1)
Since we want to be able to control how quickly we spin the crosshair, we will multiply the variable aim_sensitivity with 1. The variable itself tells us how many pixels / frame we move our crosshair. In order to make sure we don’t overflow or underflow (a circle can’t have more than 360° and less than 0°). (img. 2)
Finally, we set the x and y positions of the crosshair with our formulas (see previous chapter - how to approach the problem), and add it to the x and y positions of the character. (img. 3)
Bonus feature: Shooting
We’ve now created the aiming system correctly, but what good is it if you can’t use it to actually shoot? ![]() For this reason, I will be implementing shooting to complete this tutorial. We didn’t cover this aspect in the previous chapter because the tools to create it in code already exist, so ther is no need to go over the theory of how it works.
For this reason, I will be implementing shooting to complete this tutorial. We didn’t cover this aspect in the previous chapter because the tools to create it in code already exist, so ther is no need to go over the theory of how it works.
I will be using the built-in Darts extension.
To fire the dart, we’ll be using the A (space) button. First we create our dart, and initialize it by setting it’s position to the player’s. We also need to set it’s gravity to 0 as we are on a 2D plane. (img. 1)
Now we can set the power of the dart to any number. The power will determine it’s speed. (img. 2)
Finally, we set the angle of the dart to the inverted value of degrees and throw it. (img. 3)
And here we are, we can now shoot from the character using our crosshair!
Summary
In this tutorial, I explained the problem of many shooter games such as Blocky Boss battle (img. 1) that seems to be unresolved still. The games are very fun to play, don’t get me wrong - but the aiming is difficult since the stream of projectiles is fixated in a straight line.
We walked through my solution to the said problem, a 360° aiming system. We made use of some math formulas to convert degrees to x, y coordinates. (img. 2 & 3)
And there we are, you’ve made it to the end. Since you’re one of the few curious and willful individuals that made it to the end, I can only congradulate you for you compassion. I’ve left a little poll for you here, feel free to fill it out, but you should also feel free to leave a reply down below to keep the discussion going. I’m always open to feedback, criticism or advice to improve.
- More tutorials, expanding on this topic
- More smaller tutorials, covering basic aspects of MakeCode
- More general tutorials, covering other topics
- Less bigger, more polished lenghty tutorials
- I don’t want more tutorials
Thank you for following along, and I’ll see you next time.
Special thanks
@jwunderl for creating the Arcade sprite utils extension
@henrym for creating Blocky boss battle - the inspiration for this post
@AlexK for inspiring this post format